Axiomatization
This section introduces the specifications for BOT.
Namespace
The namespace for BOT terms is https://w3id.org/bot#
The suggested prefix for the BOT namespace is bot
The Turtle version of the BOT ontology is available at http://www.w3id.org/bot/bot.ttl
Overview of Classes and Properties
Classes: bot:Building , bot:Element , bot:Interface , bot:Site , bot:Space , bot:Storey , bot:Zone
Object Properties: bot:adjacentElement , bot:adjacentZone , bot:containsElement , bot:containsZone , bot:interfaceOf , bot:intersectingElement , bot:intersectsZone , bot:has3DModel , bot:hasBuilding , bot:hasElement , bot:hasSubElement , bot:hasSpace , bot:hasStorey , bot:hasZeroPoint
Datatype Properties: bot:hasSimple3DModel
Zones and sub-zones
Overview and Examples
Zones are defined as a part of the physical world or a virtual world that is inherently both located in this world and has a 3D spatial extent. Four sub types of Zones are defined:
- Site: An area containing one or more buildings;
- Building: An independent unit of the built environment with a characteristic spatial structure;
- Storey: A level part of a building;
- Space: A limited three-dimensional extent defined physically or notionally.
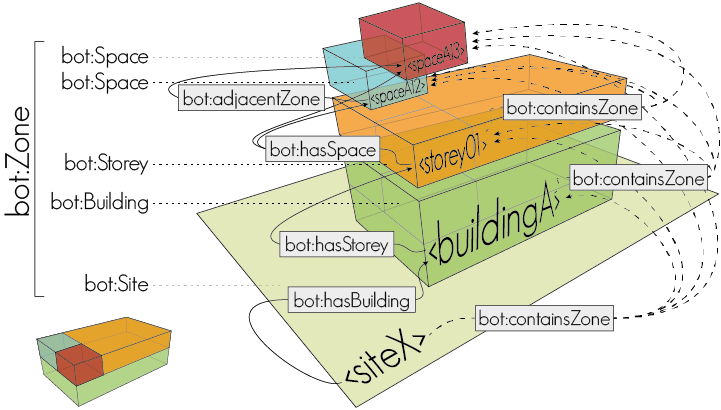
Zones must be understood as a Matryoshka doll principle. The bot:Site
instance, <siteX>, contains one building, <buildingA>, specified by the
bot:hasBuilding relationship. <buildingA> contains one storey, <storey01>,
specified by the bot:hasStorey relationship. <storey01>
contains two spaces, <spaceA12> and <spaceA13>, specified by the
bot:hasSpace relationship.
- Spaces <spaceA12> and <spaceA13> are adjacent, which is specified by the
bot:adjacentZonerelationship. - The transitive
bot:containsZonerelationship is a super-property of bothbot:hasBuilding,bot:hasStoreyandbot:hasSpace- therefore <siteX> contains all the otherbot:Zoneinstances. - A stairwell would be modeled as a
bot:Zone, linked to the differentbot:Storeys through thebot:intersectsZonerelation.
This specification does not restrict what an instance of the bot:Zone class can be. BOT may be used in conjunction with other ontologies to specify this. Examples include:
- A category of zones (e.g., office building)
- A specification of zones (e.g., office buildings with energy efficiency class above A)
- An actual zone (e.g., the kitchen in Marc's home)
Specification
This section introduces the following classes and properties:
bot:adjacentZone, bot:Building, bot:containsZone, bot:hasBuilding, bot:hasSpace bot:hasStorey, bot:intersectsZone, bot:Site, bot:Space, bot:Storey, bot:Zone,
bot:Zone
IRI: https://w3id.org/bot#Zone
a OWL Class
Zone - A part of the physical world or a virtual world that is inherently both located in this world and has a 3D spatial extent; Sub-classes of bot:Zone include bot:Site, bot:Building, bot:Storey, or bot:Space. An instance of bot:Zone can contain other bot:Zone instances, making it possible to group or subdivide zones. An instance of bot:Zone can be adjacent to or intersecting other bot:Zone instances. Finally, a bot:Zone can instantiate three relations to bot:Element, which are either contained in (bot:containsElement), adjacent to it (bot:adjacentElement) or intersecting (bot:intersectingElement).| Example | A site, a building, a space, an appartment or a fire cell. |
|---|---|
| Disjoint with | bot:Element, bot:Interface |
bot:Site ⊑ bot:Zone
IRI: https://w3id.org/bot#Site
a OWL Class
Site - A part of the physical world or a virtual world that is inherently both located in this world and having a 3D spatial extent. It is intended to contain or contains one or more buildings.| Example | A hospital campus or a single family residential lot. |
|---|---|
| Sub class of | bot:Zone |
| Disjoint with | bot:Building, bot:Storey, bot:Space |
bot:Building ⊑ bot:Zone
IRI: https://w3id.org/bot#Building
a OWL Class
Building - An independent unit of the built environment with a characteristic spatial structure, intended to serve at least one function or user activity [[ISO-12006]]. A bot:Building is a part of the physical world or a virtual world that is inherently both located in this world and having a 3D spatial extent, is contained in a building site, and can contain one or more storeys that are vertically connected.| Example | A hospital or an office building. |
|---|---|
| Sub class of | bot:Zone |
| Disjoint with | bot:Site, bot:Storey, bot:Space |
bot:Storey ⊑ bot:Zone
IRI: https://w3id.org/bot#Storey
a OWL Class
Storey - A part of the physical world or a virtual world that is inherently both located in this world and having a 3D spatial extent. A bot:Storey is contained in one or more buildings, and is intended to contain one or more spaces that are horizontally connected. Storeys of a building are connected by means of vertical connections such as elevators and stairs. A bot:Storey encompasses both zones above and below ground, for example, a building with 21 floors above ground, one ground floor and 3 basements is equal to the sentence: A building has 25 instances of bot:Storey.| Example | The ground floor. |
|---|---|
| Sub class of | bot:Zone |
| Disjoint with | bot:Site, bot:Building, bot:Space |
bot:Space ⊑ bot:Zone
IRI: https://w3id.org/bot#Space
a OWL Class
Space - A part of the physical world or a virtual world whose 3D spatial extent is bounded actually or theoretically, and provides for certain functions within the zone it is contained in.| Example | A classroom or a kitchen. |
|---|---|
| Sub class of | bot:Zone |
| Disjoint with | bot:Site, bot:Building, bot:Storey |
bot:containsZone
IRI: https://w3id.org/bot#containsZone
a OWL Object Property
contains zone - Relationship to the subzones of a major zone. A space zone could for instance be contained in a storey zone which is further contained in a building zone. bot:containsZone is a transitive property. This implies that in the previous example a bot:containsZone relationship holds between the space zone and the building zone.| Domain | bot:Zone |
|---|---|
| Range | bot:Zone |
| Domain Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| Range Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| is Transitive | |
bot:hasBuilding ⊑ bot:containsZone
IRI: https://w3id.org/bot#hasBuilding
a OWL Object Property
has building - Relation to buildings contained in a zone. The typical domains of bot:hasBuilding are instances of bot:Site.| Sub property of | bot:containsZone |
|---|---|
| Domain | bot:Zone |
| Range | bot:Building |
| Domain Includes | bot:Site |
bot:hasStorey ⊑ bot:containsZone
IRI: https://w3id.org/bot#hasStorey
a OWL Object Property
has storey - Relation to storeys contained in a zone. The typical domains of bot:hasStorey are instances of bot:Building.| Sub property of | bot:containsZone |
|---|---|
| Domain | bot:Zone |
| Range | bot:Storey |
| Domain Includes | bot:Building |
bot:hasSpace ⊑ bot:containsZone
IRI: https://w3id.org/bot#hasSpace
a OWL Object Property
has space - Relation to spaces contained in a zone. The typical domains of bot:hasSpace are instances of bot:Storey or bot:Building.| Sub property of | bot:containsZone |
|---|---|
| Domain | bot:Zone |
| Range | bot:Space |
| Domain Includes | bot:Building, bot:Storey |
bot:adjacentZone
IRI: https://w3id.org/bot#adjacentZone
a OWL Object Property
adjacent zone - Relationship between two zones that share a common interface, but do not intersect.| Domain | bot:Zone |
|---|---|
| Range | bot:Zone |
| Domain Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| Range Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| Disjoint object properties | bot:intersectsZone |
| is Symmetric | |
bot:intersectsZone
IRI: https://w3id.org/bot#intersectsZone
a OWL Object Property
intersects zone - Relationship between two zones whose 3D extent intersect. For example, a stairwell intersects different storeys.| Domain | bot:Zone |
|---|---|
| Range | bot:Zone |
| Domain Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| Range Includes | bot:Site, bot:Building, bot:Storey, bot:Space |
| Disjoint object properties | bot:adjacentZone |
| is Symmetric | |
Elements
Overview and Examples
Building elements are physical parts of building constructions. Examples of elements include walls, doors, pipes, heaters, lights, smart sensors, tables, chairs.
Elements can contain sub elements. Zones can contain elements, or be adjacent to elements.
This specification does not restrict what an instance of the bot:Element class can be. BOT may be used in conjunction with other ontologies to specify this. Examples include:
- A category of elements (e.g., air conditioner with class A energy efficiency ratio)
- A specification of elements (e.g., air conditioner with energy efficiency ratio above B)
- A element in a specific catalogue (e.g., air conditioner with reference xyz manufactured by abc)
- An actual element (e.g., the air conditioner Marc installed yesterday at his home)
Specification
This section introduces the following classes and properties:
bot:Element
IRI: https://w3id.org/bot#Element
a OWL Class
Element - Constituent of a construction entity with a characteristic technical function, form or position [[[ISO-12006]], 3.4.7].| Example | Any product or device that is described in its context of a building. For example a wall, a chair or a temperature sensor. |
|---|---|
| Disjoint with | bot:Zone, bot:Interface |
bot:hasSubElement
IRI: https://w3id.org/bot#hasSubElement
a OWL Object Property
hosts element - Relation between two building elements, either one element hosting another (e.g. a wall hosts a window) or a subcomposition of a building element into smaller parts (e.g. an air handling unit has as a part a fan).| Example | <wall> bot:hasSubElement <window> . |
|---|---|
| Domain | bot:Element |
| Range | bot:Element |
bot:hasElement
IRI: https://w3id.org/bot#hasElement
a OWL Object Property
has element - Links a Zone to an Element that is either contained in, adjacent to or intersecting with the Zone. The intended use of this relationship is not to be stated explicitly, but to be inferred from its sub-properties. It will, for example, allow one to query for all the doors of a building given that they have an adjacency to spaces of the building.| Domain | bot:Zone |
|---|---|
| Range | bot:Element |
| Sub property of Chain | bot:containsZone o bot:hasElement |
bot:containsElement ⊑ bot:hasElement
IRI: https://w3id.org/bot#containsElement
a OWL Object Property
contains element - Relation to a building element contained in a zone.| Sub property of | bot:hasElement |
|---|---|
| Sub property of Chain | bot:containsZone o bot:containsElement |
bot:adjacentElement ⊑ bot:hasElement
IRI: https://w3id.org/bot#adjacentElement
a OWL Object Property
adjacent element - Relation between a zone and its adjacent building elements, bounding the zone.| Sub property of | bot:hasElement |
|---|---|
| Disjoint object properties | bot:intersectingElement |
bot:intersectingElement ⊑ bot:hasElement
IRI: https://w3id.org/bot#intersectingElement
a OWL Object Property
intersecting element - Relation between a Zone and a building Element that intersects it.| Sub property of | bot:hasElement |
|---|---|
| Disjoint object properties | bot:adjacentElement |
Interfaces
Overview and Examples
Interfaces are used in situations where it is necessary to quantify a relationship between two elements or zones or an element and a zone. The following figure provides an overview of the core classes and properties that are specifically related to modeling Interfaces.
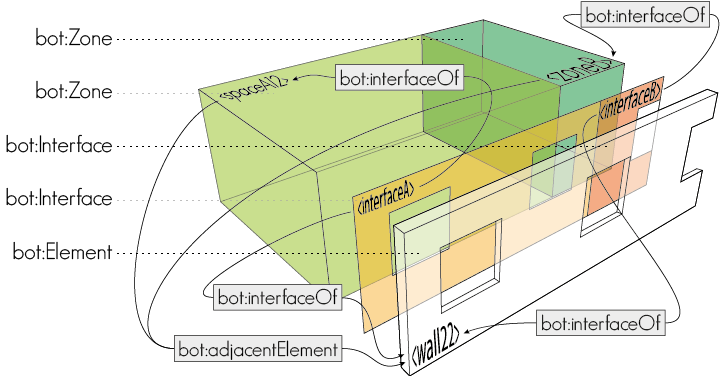
In the figure, there are two
bot:Zone instances that are both adjacent to the same
bot:Element instance <wall22>. To quantify
the heat transfer areas between <spaceA12>/<wall22> and <zoneB>/<wall22>
respectively, two interfaces, <interfaceA> and <interfaceB>, are introduced.
Both interfaces are related to <wall22> through the bot:interfaceOf
relationships, but their second bot:interfaceOf relationship is to
either <spaceA12> or <zoneB>.
Specification
This section introduces the following classes and properties:
bot:Interface
IRI: https://w3id.org/bot#Interface
a OWL Class
Interface - A generic concept to qualify the relationship of two or more things in the world, where at least one is a building element or zone. Examples: (1) Qualification of heat transmission between zones through one or more building elements. This includes one-dimensional (surface) heat losses from one zone to another through a single building element, a two dimensional (line) loss from one zone to another through the connection in which the two elements meet or a three dimensional (point) loss from one zone to another through the connection where three elements (typically two walls and a slab) meet. (2) Connection of an electric device to the electric system of a building. (3) A door between one room and another.| Example | A heat transfer area between a space and an adjacent wall, the pipe surface facing the space that the pipe passes through, a joint between two concrete elements or connection between a window and a wall. |
|---|---|
| Disjoint with | bot:Zone, bot:Element |
bot:interfaceOf
IRI: https://w3id.org/bot#interfaceOf
a OWL Object Property
interface of - Relationship between an interface and another thing (building zone, element or owl:Thing).| Domain | bot:Interface |
|---|---|
| Range Includes | bot:Zone, bot:Element |
3D Model
Overview and Examples
Any bot:Zone or bot:Element can be assigned a 3D Model (including geometry, material, etc.), using some existing data format for 3D models. Two properties are defined for this:
- The
bot:hasSimple3DModeldatatype property links abot:Zoneorbot:Elementto a 3D Model encoded as a literal. Note that we encourage the use of URIs for mediatype with the IANA authority. For examplehttps://www.iana.org/assignments/media-types/model/3mffor the mediatypemodel/3mf. Other mediatypes for OBJ, STP, IFC, W3D, etc. can be defined. If the data format is textual, then the lexical form of the 3D Model literal SHOULD be encoded as a Unicode [[!UNICODE]] string, which SHOULD be in Normal Form C [[!NFC]]. If the data format is binary, then the lexical form of the 3D Model literal SHOULD be encoded using a base32 encoding [[!rfc4648]]. - The
bot:has3DModelobject property links abot:Zoneorbot:Elementto some IRI that identifies a 3D Model. This 3D Model can then be described using some dedicated RDF vocabulary. Else, the 3D Model IRI could be dereferenceable, and when looking up the IRI one could retrieve a representation of the 3D Model with some existing data format for 3D models.
Specification
This section introduces the following classes and properties:
bot:hasZeroPoint
IRI: https://w3id.org/bot#hasZeroPoint
a OWL Object Property
has Zero Point - Links a bot:Site to an instance that encodes the latitude and longitude of the Zero Point of the building site. This could be an instance of awgs84:Point. The definition of GIS and geometry is not within the scope of BOT and an appropriate ontology needs to be selected here by the user. The use of this property is potentially ambiguous and it might be removed or revised in future editions of the ontology.
| Domain | bot:Site |
|---|
bot:hasSimple3DModel
IRI: https://w3id.org/bot#hasSimple3DModel
a OWL Datatype Property
has Simple 3D Model - Links any bot:Zone or bot:Element to a 3D Model encoded as a literal.| Domain Includes | bot:Zone | bot:Element |
|---|
bot:has3DModel
IRI: https://w3id.org/bot#has3DModel
a OWL Object Property
has 3D Model - Links any bot:Zone or bot:Element to a IRI that identifies its 3D Model. This 3D Model can then be described using some dedicated RDF vocabulary. Else, the 3D Model IRI could be dereferenceable, and when looking up the IRI one could retrieve a representation of the 3D Model with some existing data format for 3D models.| Domain Includes | bot:Zone | bot:Element |
|---|